Network Analysis and Simulations: Six Degrees of Francis Bacon
These visualisations, developed by Brian Ball, Tyler Gore, Marta Weber, and Peter West at Northeastern University London, present the findings of research carried out as part of the FY25 TIER 1 funded project New Digital Methods for Understanding the Impacts of Early Women Writers on Science and Philosophy.
This project is a London-Boston, collaborative project between Northeastern University London, the PolyGraphs project, the NULab, and the Women Writers Project (the project PIs are Sarah Connell, Julia Flanders, Brian Ball, and Peter West). The project examines and highlights the impacts of early women scientists and natural philosophers on the development of these disciplines during a formative period of the Enlightenment. The project takes Margaret Cavendish’s (1623–1673) engagements with the Royal Society as a case study in the relation between early women’s writing and early institutional science.
As part of this project, the team in London employed network analysis and computer network simulations to evaluate the status of women in early modern intellectual networks. Specifically, the team focused on the relationship between Cavendish and the founding members of the Royal Society. The primary database for this research was the Six Degrees of Francis Bacon Project project. Six Degrees of Francis Bacon is a digital reconstruction of a network consisting of 13,309 ‘nodes’ (i.e., historical figures) and the ‘edges’ that connect them to one another. In turn, the information about these nodes and the edges between them is drawn from the Oxford Dictionary of National Biography.
The visualisations below represent two kinds of findings of this networks research. First, findings pertaining to the status of women in the Six Degrees of Francis Bacon network. Second, findings of computer network simulations carried out in order to evaluate the impact of the structure of intellectual networks on the transfer of knowledge.
Gender Analysis
Drawing inspiration from the late Helen de Cruz who suggested that something like the ‘Bechdel test’, usually applied to films, might be applied to philosophy and history of philosophy research, this visualisation (Figure One) shows how many women in the Six Degrees network only share edges with men. There are a total of 12,068 men in the network and 966 women. When men are removed from the network, 358 women are left as isolated nodes with no direct edges.
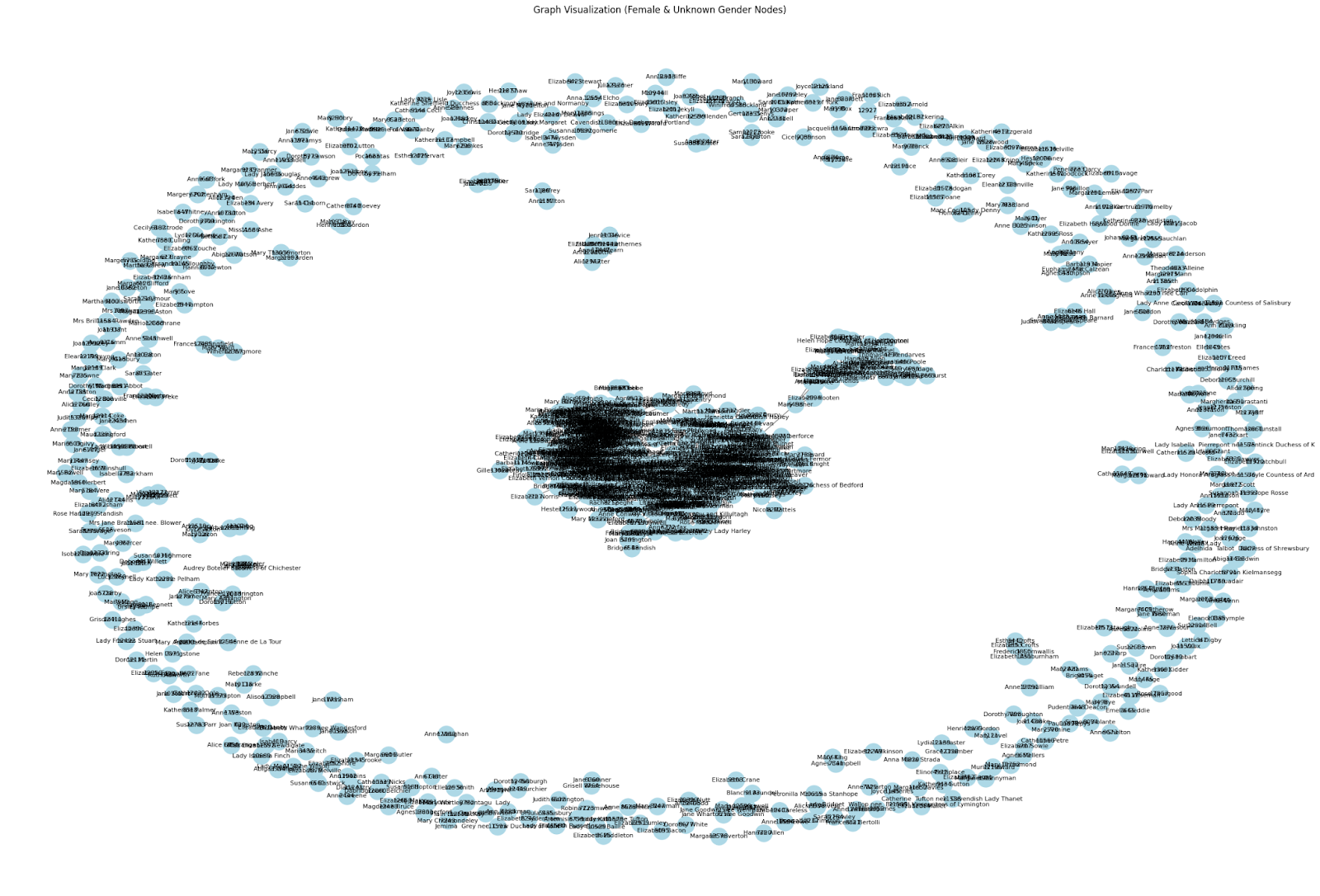
This image depicts the Six Degrees of Francis Bacon network, once all the men in the network have been removed.
- There are 966 women (7.4%) and 12,068 men total in the network (82.6%)
- 358 women are rendered totally isolated; they are only connected to men
- 37.1% of women are connected only to men
- In comparison, only 0.4% of men are only connected to women
See the full resolution image and an annotated version of the image.
Further analysis of the status of women in the Six Degrees network revealed that 88.8% of women in the network are in a relationship of what Sangiacomo and Beers call ‘familiar strangers’. To be in a relation of ‘familiar stranger’ is for two individuals to be connected to a third, but not connected to one another. So, if A and B both know C, but do not know one another, then A and B are ‘familiar strangers’. The findings below (Figure Two) thus further emphasize the degree to which women in the network are more likely to be connected to men than other women. The most well connected women in the network (perhaps unsurprisingly) are monarchs and women of very high social standing (Figure Three).
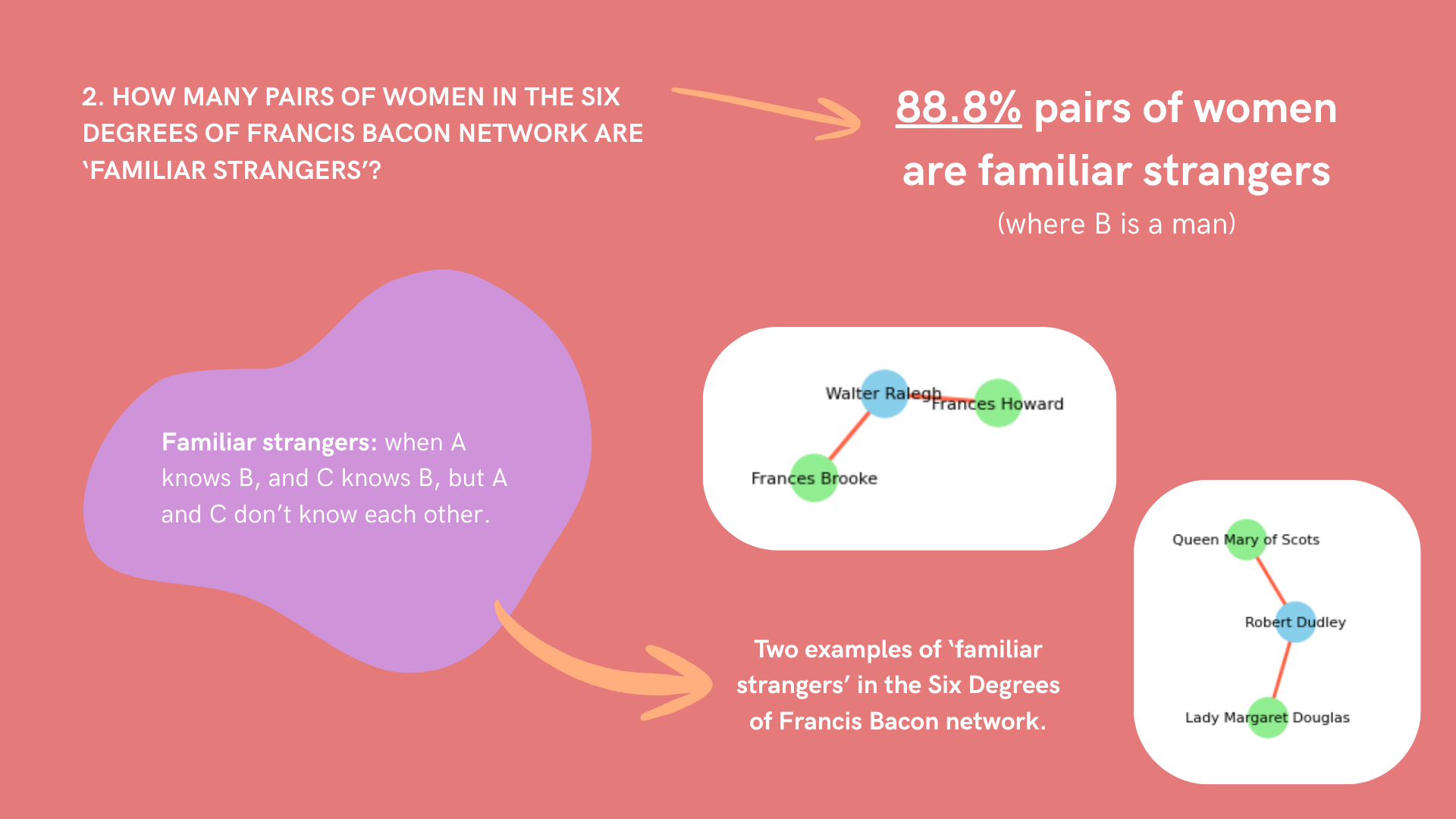
Familiar strangers is a term referring to when: person A knows person B, and person C knows B, but person A and C don’t know each other. In the Six Degrees of Francis Bacon Network, 88.8% of pairs of women are familiar strangers (where person B is a man).
Two examples of familiar strangers in the network are shown. Frances Brooke and Frances Howard are connected by Walter Ralegh, but aren’t directly connected to each other. Queen Mary of Scots and Lady Margaret Douglass are similarly connected by Robert Dudley.
See the full resolution image.
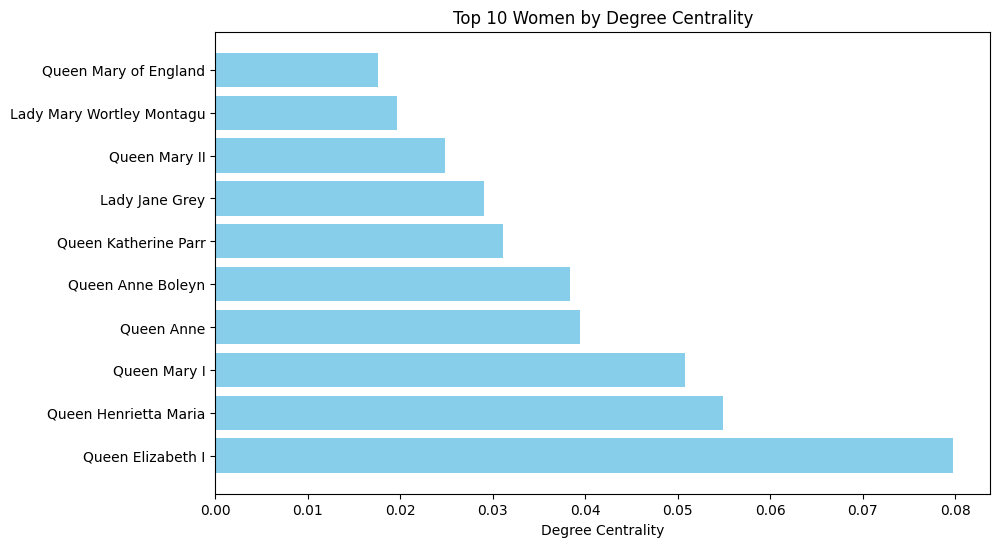
The best connected women (those with the highest ‘degree centrality’) are Queens and Ladies with very high social standing.
See the full resolution image and an annotated version of the image.
This visualisation (Figure Four) focuses specifically on Cavendish’s connections within the Six Degrees network. The image presents an ‘ego network’, i.e., a series of nodes and edges, from within the wider Six Degrees network, which are all connected to Cavendish. It is worth observing that, in line with the wider findings of women’s connections in the network, the majority (16 out of 68 nodes) of Cavendish’s connections are with men.
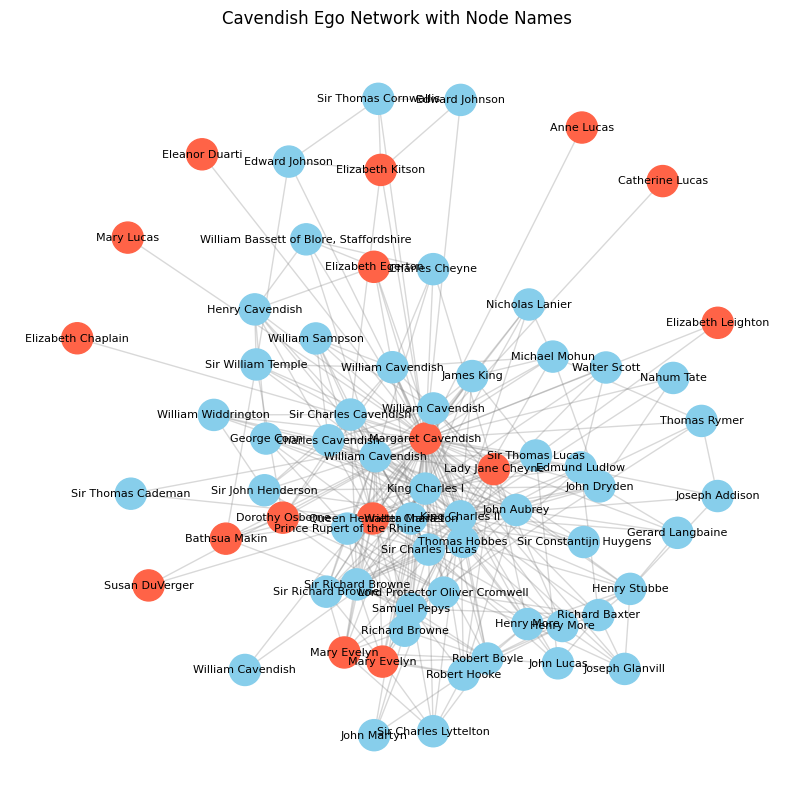
This image shows Cavendish’s ‘ego network’; it depicts those figures in the Six Degrees of Francis Bacon network who are directly connected (i.e., share an ‘edge’) with Cavendish. Those in red are women, those in blue are men.
See the full resolution image and an annotated version of the image.
Simulating Knowledge Transfer
The second set of visualisations (Figures Five through Fourteen) represent the findings of computer network simulations that focus on Cavendish’s connections to the founding members of the Royal Society: William Brouncker (c.1620–1684), Robert Boyle (1627–1691), Robert Hooke (1635–1703), Henry Oldenburg (c.1618–1677), William Petty (1623–1687), John Wilkins (1614–1672), Christopher Wren (1632–1723), and Prince Rupert of the Rhine (1619–1682). Note that Prince Rupert does not appear in the first visualisation as he does not share any edges with other founding members in the Six Degrees network.
In four steps, these visualisations depict the findings of simulations that were carried out on three variations of this sub-network extracted from the wider Six Degrees network. The first network contains simply the founding members of the Royal Society listed above. The second contains the founding members plus Cavendish; in this variation, Cavendish retains her historically accurate connections (as per the Six Degrees data) to those founding members (so if she is not connected to a founding member in the wider Six Degrees network, then she is not connected to them here). The third variation is also the founding members plus Cavendish, but here Cavendish is connected, i.e., shares an edge with every other member. Roughly speaking, the aim was to speculatively assess how the transfer of knowledge within the Royal Society network may have been different if (a) Cavendish was also a founding member, and (b) if Cavendish was an especially well-connected founding member.
Roughly speaking, the simulations we employed work on the assumption that there is a ‘truth’ that each member of the network has a certain degree of belief in. For instance, let’s assume that each individual is working out whether they believe in the truth of the proposition a certain coin is weighted towards heads. Each step in the simulation is an opportunity (in this scenario) for each individual to flip the coin and re-assess their level of belief in that claim. What’s important is that individuals are able to consult with others they are connected to—and e.g., share their own beliefs. What our findings indicate is that better connected individuals (‘nodes’ in the network with more ‘edges’) on average reach the truth in fewer steps than those who are less well-connected.
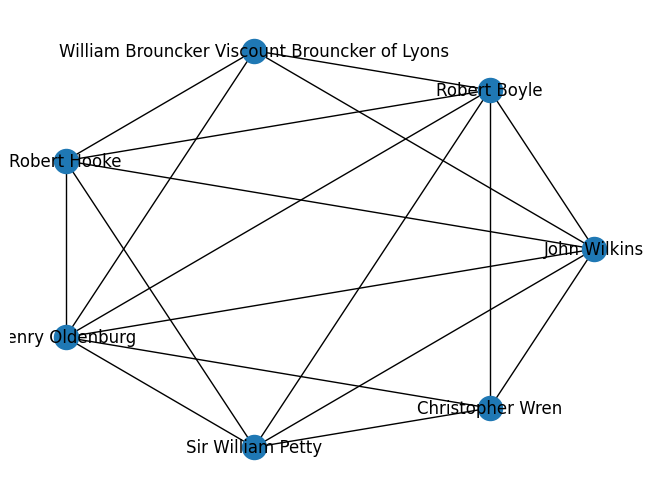
Founding Members of the Royal Society
This image shows the connections (‘edges’) in a network made up of the founding members of the Royal Society.
Prince Rupert of the Rhine is not shown since he has no shared connections with other nodes.
See the full resolution image and an annotated version of the image.
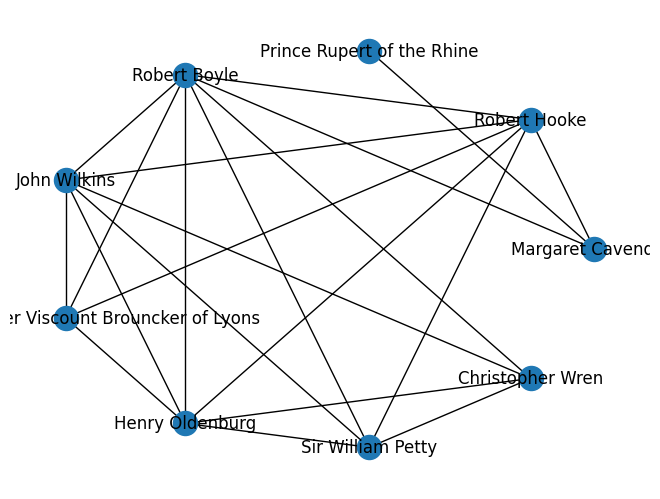
Founding Members of the Royal Society (with Cavendish)
This image shows the connections (‘edges’) in a network made up of the founding members of the Royal Society, as well as Cavendish (with historically accurate edges).
See the full resolution image and an annotated version of the image.

Founding Members of the Royal Society (with Cavendish connected)
This image shows the connections (‘edges’) in a network made up of the founding members of the Royal Society and Cavendish, where Cavendish is connected to everyone else in the network.
See the full resolution image and an annotated version of the image.
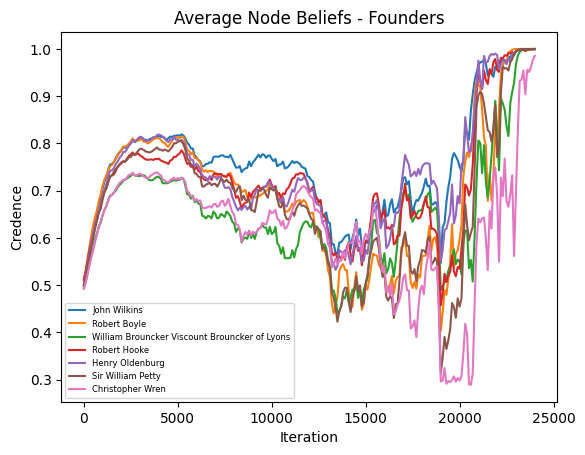
Founding Members of the Royal Society
This image shows each founding member’s average level of belief in the truth, measured across the various simulations we ran. On average, John Wilkins’s average belief in the truth is highest, while Christopher Wren’s is lowest.
See the full resolution image and an annotated version of the image.
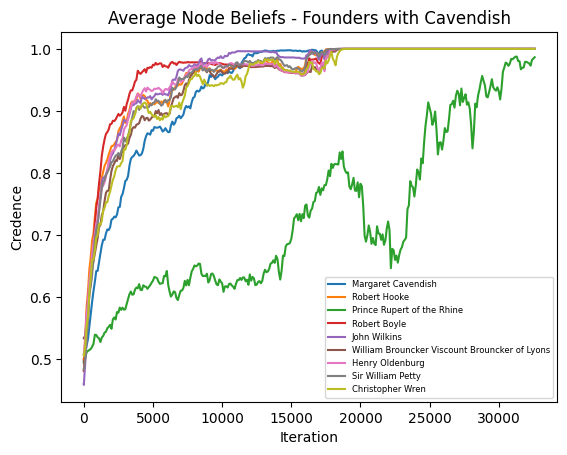
Founding Members of the Royal Society (with Cavendish)
This image shows the average belief of members of the network where Cavendish is part of the network but retains her historically accurate edges. Cavendish’s average belief is much higher than Prince Rupert of the Rhine’s, but lower than several other members of the network.
See the full resolution image and an annotated version of the image.
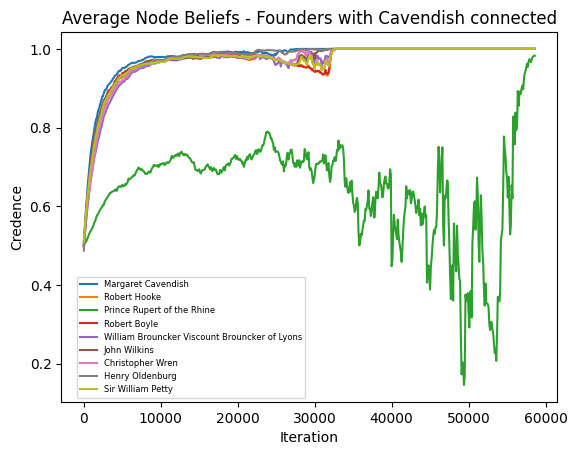
Founding Members of the Royal Society (with Cavendish connected)
This image shows the average beliefs where Cavendish is connected to everyone in the network. In this network, Cavendish’s belief is, on average, highest.
See the full resolution image and an annotated version of the image.
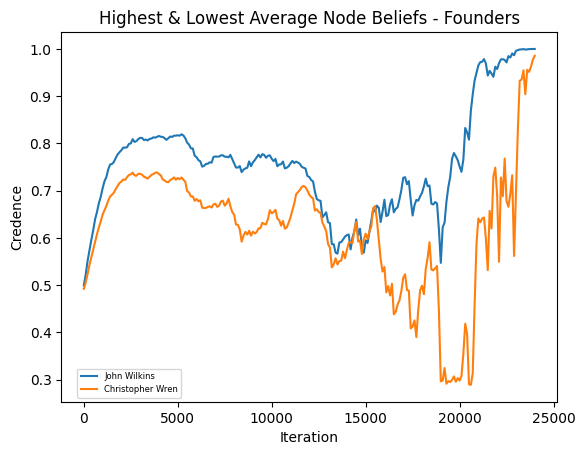
Founding Members of the Royal Society
This image shows the founding members of the Royal Society with the highest average belief in the truth (Wilkins) and the lowest average belief (Wren).
See the full resolution image and an annotated version of the image.
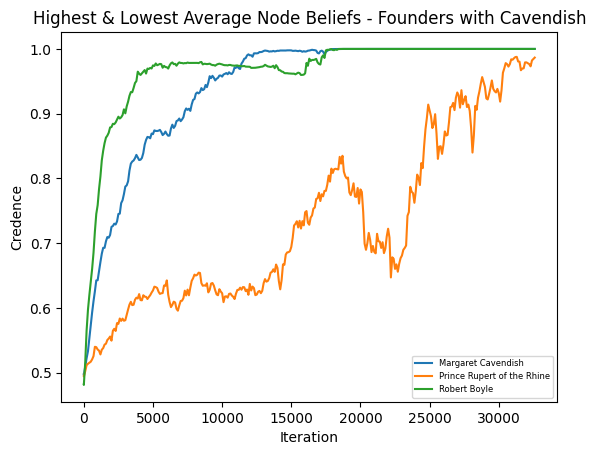
Founding Members of the Royal Society (with Cavendish)
This image shows the members of the network with highest (Robert Boyle) and lowest (Prince Rupert) average belief in the truth once Cavendish is added to the network with her historically-accurate connections. Cavendish’s beliefs are also plotted for reference.
See the full resolution image and an annotated version of the image.
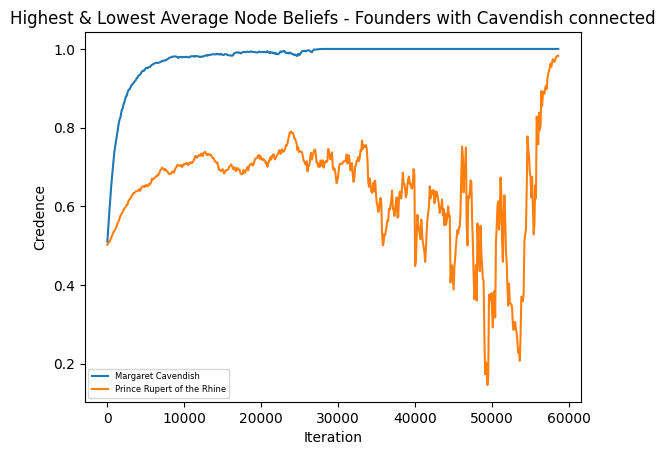
Founding Members of the Royal Society (with Cavendish connected)
This image shows the members of the network with the highest and lowest average beliefs in the truth where Cavendish is connected to everyone in the network. Note that Cavendish has the highest average belief in the truth.
See the full resolution image and an annotated version of the image.

